尺度函数,探索科技发展的新维度

尺度函数：揭秘数学世界的神奇密码

亲爱的读者，你是否曾在数学的世界里迷失方向，对那些复杂的公式和理论感到困惑？今天，我要带你走进一个神奇的世界——尺度函数，它就像一把钥匙，能解锁数学世界的神秘之门。

什么是尺度函数？

尺度函数，顾名思义，是一种具有尺度变换性质的函数。它最早由德国数学家埃米·诺特提出，并在数学分析、信号处理等领域有着广泛的应用。简单来说，尺度函数就是一组具有特定性质的函数，它们在尺度变换下保持不变。

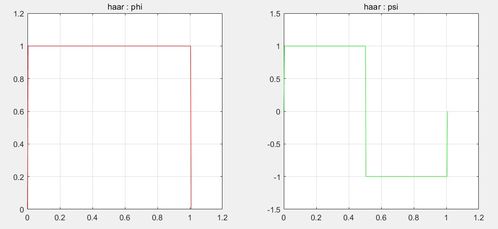
尺度函数的神奇之处

1. 线性组合

尺度函数的一个重要特性是线性组合。这意味着，任何尺度函数都可以通过线性组合得到。这种特性使得尺度函数在信号处理领域有着广泛的应用，如小波变换、滤波器设计等。

2. 尺度变换

尺度函数在尺度变换下保持不变，这是其最神奇的地方。想象你手中拿着一张地图，当你放大或缩小地图时，地图上的比例尺会发生变化，但地图上的内容却保持不变。尺度函数也是如此，无论你如何改变尺度，函数的形状和性质都不会改变。

3. 逼近性质

尺度函数还具有逼近性质。这意味着，任何连续函数都可以通过尺度函数的线性组合来逼近。这种性质在数值分析、图像处理等领域有着重要的应用。

尺度函数的应用

1. 信号处理

在信号处理领域，尺度函数被广泛应用于小波变换。小波变换是一种时频分析工具，它可以将信号分解为不同频率和尺度的成分。尺度函数作为小波变换的基础，对于信号处理具有重要意义。

2. 图像处理

在图像处理领域，尺度函数被用于图像压缩、去噪、边缘检测等。通过尺度函数，我们可以将图像分解为不同尺度的成分，从而实现图像的优化处理。

3. 数值分析

在数值分析领域，尺度函数被用于求解偏微分方程、优化问题等。尺度函数的逼近性质使得它在数值分析中具有广泛的应用前景。

尺度函数的未来

随着科学技术的不断发展，尺度函数在各个领域的应用越来越广泛。未来，尺度函数有望在更多领域发挥重要作用，如量子计算、生物信息学等。相信在不久的将来，尺度函数将成为数学世界的一颗璀璨明珠。

尺度函数，这个看似神秘的数学概念，其实在我们的生活中有着广泛的应用。它不仅揭示了数学世界的神奇密码，还为各个领域的研究提供了有力的工具。让我们一起走进尺度函数的世界，感受数学的魅力吧！